Zadania
Zad. 1. Boki trójkąta tworzą postęp arytmetyczny z różnicą r . Stosunek pola tego trójkąta do pola prostokąta, utworzonego z dwóch mniejszych boków trójkąta, jest m. Znaleźć boki trójkąta i przeprowadzić dyskusję.
Zad. 2. Na wysokości stożka, równej h , o promieniu podstawy R, opisano jako na średnicy kulę. W jakiej odległości od podstawy stożka należy poprowadzić płaszczyznę prostopadłą do wysokości, aby różnica pól przekrojów kul i stożka tą płaszczyzną była równa wielkości danej πa2. Znaleźć warunki możliwości zadania oraz ilość rozwiązań, uwzględnić że a może być ujemne.
Zad. 3. Obywatel przebywał zwykle drogę z majątku do miasta w ciągu 3-ch godzin; ponieważ droga była zepsuta, więc jechał o 2 klm. mniej na godzinę. Ujechawszy połowę drogi, zmienił konie i jechał o 1 klm. prędzej, niż poprzednio; w ten sposób przybył do miasta o a godzin prędzej, niż gdyby jechał, nie zmieniając koni.
1) Znaleźć odległość majątku od miasta;
2) znaleźć warunek możliwości zadania i 3) ilość rozwiązań.
Zad. 4. W kole o środku O i promieniu R, poprowadzono dwie prostopadłe średnice AA1 i BB1. Wyznaczyć na okręgu punkt M tak, że mamy zależność AC = m·BD , gdzie punkt C i punkt D są rzutami punktu M odpowiednio na średnice AA1 i BB1, a m dana liczba dodatnia. Dyskusja w stosunku do m. Do jakiego położenia granicznego dąży punkt M, gdy liczba m zwiększa się nieograniczenie.
Zad. 5. Znaleźć dwie liczby posiadające następujące własności.
1) różnica ich równa się iloczynowi, zmniejszonemu o a;
2) suma kwadratów równa się iloczynowi, zwiększonemu o a .
Dyskusja:
1) jakie powinno być a, aby wszystkie rozwiązania były rzeczywiste;
2) ile najwyżej może być rozwiązań z dodatniemi wartościami obu liczb;
3) czy mogą być wszystkie rozwiązania urojone?
Zad. 6. W równaniu dwukwadratowem x4 — (3m + 4) x2 + (m + l)2 = 0 określić m pod warunkiem, że pierwiastki tego równania będą stanowić wyrazy postępu arytmetycznego.
Zad. 7. Zbadać przebieg zmienności funkcji Sin2α — Cos2α, gdy α zmienia się od 0° do 180°.
Zad. 8. Znaleźć wymiary prostokąta ABCD, mając dany jego obwód 2p oraz promień koła, które przechodzi przez wierzchołki A i B i jest styczne do boku CD . Przedyskutować zadanie.
Szkice rozwiązań


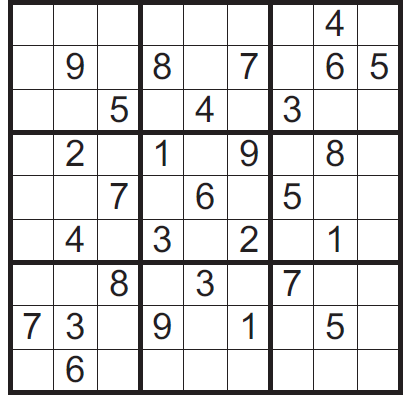
 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.


