Zadania
Zad. 1. (typ humanistyczny) W punktach przecięcia się koła X2 + Y2 = 16 i elipsy
(X/5)2 + (Y/3)2 = 1 nakreślić styczne do koła i elipsy i obliczyć kąt, który te styczne tworzą ze sobą.
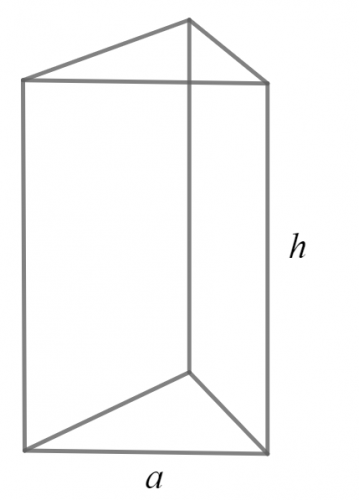
Zad. 2. (typ humanistyczny) Powierzchnia graniastosłupa prostego, mającego za podstawę trójkąt równoboczny, a wysokość h = 1 dm, wynosi p = 17,4 dm2. Obliczyć krawędź podstawy tego graniastosłupa.
Zad. 3. (typ klasyczny) Trzy liczby tworzą szereg geometryczny; suma ich równa się 28, a iloczyn średniego wyrazu i sumy dwóch skrajnych równa się 160. Co to za liczby?
Szkice rozwiązań
Zad. 1. Zauważmy, że sytuacje w każdej ćwirtce są analogiczne, więc możemy rozpatrzeć tylko tę z pierwszej.
Wówczas rozwiązanie układu równań tych dwóch krzywych daje punkt [tex](\frac{5\sqrt7}{4}, \frac{9}{4})[/tex].
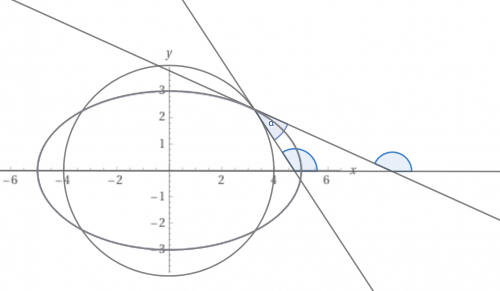
Aby wyznaczyć współczynniki kierunkowe stycznych, wystarczy wyznaczyć pochodne fukcji określających łuki okręgu i elisy w tej ćwiartce w wyznaczonym powyżej punkcie.
Otrzymujemy dla stycznej do okręgu współczynnik [tex]\frac{-5\sqrt7}{9}[/tex], dla elipsy zaś [tex]\frac{-\sqrt7}{5}[/tex].
Ze współczynników kierunkowych możemy wprost wyznaczyć kąt nachylenia stycznych do osi OX (dlaczego?).
Wynoszą one ok. 124.23° dla stycznej do okręgu oraz ok. 152,11° dla stycznej do elipsy.
Zatem kąt [tex]\alpha[/tex] ≈ 27,88°.
Zad. 2. Przyjmujemy oznaczenia z treści zadania i oznaczamy szukaną długość krawędzi podstawy przez a.Pole powierzchni graniastosłupa wynosi [tex]p=3ah+2\frac{a^2\sqrt3}{4}[/tex]. Po przyrównaniu p do 17,4 otrzymujemy równanie a2√3 + 6a – 34,8 = 0, co pozwalana na wyznaczenie a = [tex]\sqrt{27+104,4 \sqrt 3} – 3 \sqrt 3[/tex]dm. Dlaczego pomijamy drugi pierwiastek równania kwadratowego?
Zad. 3. Oznaczamy szukane liczby przez a1, a2, a3 i otrzymujemy układ równań:
a1 + a2 + a3 = 28
a2 (a1 + a3) = 160.
Pozwala to wyznaczyć a2 jako 8 lub 20. Rozważając a2 = 8 i korzystając z zależności między kolejnymi wyrazami ciągu geometrycznego (jaka to zależność?), otrzymujemy a1 = 4 i a3 = 16 lub na odwrót. Postępując analogicznie dla a2 = 20, dochodzimy do sprzeczności. Warunki zadania spełniają zatem liczby 4, 8, 16.


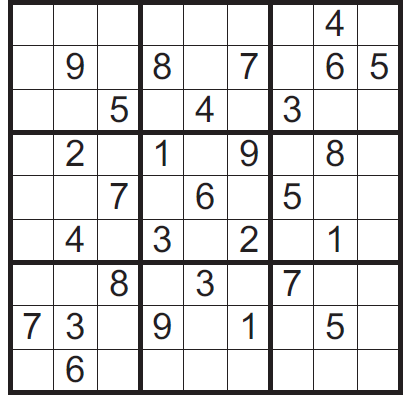
 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.


