Zadania
Zad. 1. Suma sześciu pierwszych wyrazów postępu geometrycznego jest 189, a suma następnych sześciu jest 12096. Jaki to postęp?
Zad. 2. Rozwiązać równanie:
5 sin x + 3 sin y = 4
3 (5 sin x) – 2 (3 sin y) = 5
Zad. 3. (typ humanistyczny) Jakie jest miejsce geometryczne punktów przecięcia się wysokości wszystkich trójkątów, które mają tę samą podstawę AB = c i ten sam kąt γ u wierzchołka?
Zad. 4. (typ klasyczny) Kupiec wkładał w końcu każdego roku po 3500 mk*) do banku na 3,5%, prócz tego w końcu piątego i piętnastego roku wniósł jeszcze po 5000 mk. Ile wynosi kapitał jego w końcu 20-go roku?
*) Chodzi zapewne o marki Królestwa Polskiego wprowadzone 9 XII 1916 roku na terenach zaborów niemieckiego i austriackiego (podczas konferencji w Pszczynie jesienią 1916 cesarze niemiecki oraz austro-węgierski proklamowali obietnicę utworzenie Królestwa Polskiego bez żadnych ram czasowych ani określonych granic, z własną monetą, sądownictwem i szkolnictwem). Monety te przetrwały dłużej niż samo Królestwo, gdyż pod nazwą marki polskie funkcjonowały od 11 XI 1918 do dnia reformy pieniężnej Grabskiego (czyli 29 IV 1924), kiedy marka polska została zastąpiona przez polskiego złotego.
Szkice rozwiązań
Zad. 1. Zauważmy, że a7+a8+...+a12 = a1·q6+a2·q6+...+a6·q6 = (a1+a2+...+a6)·q6. Stąd q6 = 12096/189 = 64, a q=2 lub q=-2. Z kolei a1+a2+...+a6 = a1 · (1–q6)/(1–q), więc odpowiednio a1 = 3 lub a1 = -9. Mamy zatem dwie możliwości: an = 3 · 2n-1 lub an = -9 · (-2)n-1.
Zad. 2. Podstawiając a = 5sinx i b = 3siny, można dany układ zapisać jako:
a+b = 4
3a–2b = 5.
Po rozwiązaniu tego układu otrzymujemy a = 13/5 i b = 7/5, zatem sinx = 13/25 i siny = 7/15. Zatem rozwiązaniem układu równań jest każda para liczb (x, y), dla której x ≈ 0,547 + 2kπ lub x ≈ 2,118 + 2kπ oraz y ≈ 0,486 + 2nπ lub y ≈ 2,056 + 2nπ, gdzie k i n są dowolnymi liczbami całkowitymi.
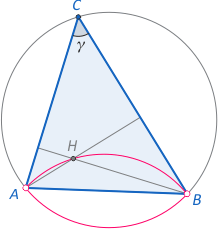
Zad. 3. Oznaczmy przez H punkt przecięcia wysokości trójkąta ABC (taki punkt nazywamy ortocentrum trójkąta). Zauważmy, że miara kąta między wysokościami trójkąta wychodzącymi z wierzchołków A i B jest stała i wynosi zawsze 180°–γ (dlaczego?). To oznacza, że punkty przecięcia wysokości dla wszystkich trójkątów leżą:
a) na łuku AHB okręgu opisanego na trójkącie ABH o podstawie AB i kącie przy wierzchołku H równym 180°–γ (z wyłączeniem punktów A i B) lub
b) na symetrycznym odbiciu tego łuku względem prostej AB.
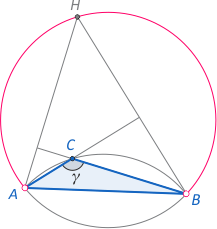
Szukanym obszarem jest więc suma dwóch symetrycznych łuków opisanych w a) i w b) bez punktów A i B. W szczególnym przypadku, gdy γ=90°, obszar ten jest okręgiem o średnicy AB, z wyłączeniem punktów A i B. Sytuację gdy γ<90° pokazuje rys. 1, a gdy gdy γ>90° - rys. 2.
 |
 |
| rysunek 1 | rysunek 2 |
Zad. 4. Zauważmy, że wpłaty coroczne (a) i dwie wpłaty dodatkowe (b i c) możemy rozpatrywać osobno jako trzy lokaty.
a) Pierwsza wpłata zdąży zaprocentować 19 razy, druga - 18 razy, ..., a dwudziesta ani razu. Tę część kapitału opisuje suma 20 wyrazów ciągu geometrycznego, w którym a1 = 3500 i q = 1,035. Zatem po 20 latach z wpłacanych corocznie pieniędzy uzyskamy kwotę 3500 · (1–1,03520) / (1–1,035) ≈ 98978,89.
b) 5000 wpłacone w końcu piątego roku zaprocentuje 15 razy, więc da dodatkową kwotę 5000 · 1,03515 ≈ 8376,744.
c) 5000 wpłacone w końcu piętnastego roku zaprocentuje 5 razy, więc da dodatkową kwotę 5000 · 1,0355 ≈ 5938,431.
Po 20 latach kapitał będzie sumą kwot z punktów a, b, c i będzie wynosił 113 294,06 mk.


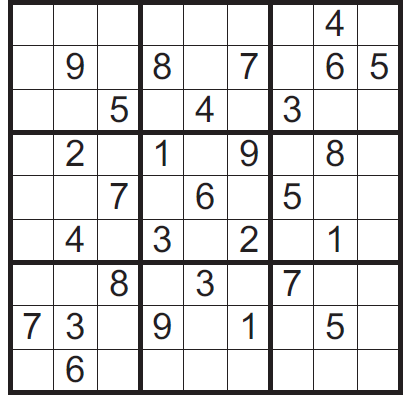
 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.


